Byers, J.A. 1992. Grid cell contour mapping of point densities: bark beetle attacks, fallen pine shoots, and infested trees Oikos 63:233-243. pdf

Program output of a random distribution of points. Download CONT-DEN.EXE for PC
See
A method for calculating and displaying patterns of local density of plants and animals is presented for use with personal computers. The algorithm, coded in the BASIC programming language, uses x,y spatial point coordinates of organisms to calculate and display a coloured or shaded map of local densities within grid cells. The radius of the local areas about the grid points within which densities are calculated, the density-class interval boundaries when colouring the cells, and the grid resolution can all he varied to facilitate exploratory investigations.
Contour density maps resulting from the method are shown for an attack distribution of the bark beetle Pityogenes chalcographus (Coleoptera: Scolytidae) on Norway spruce bark, Picea abies, and for a random distribution. Minimum allowed distance analysis of the attack distribution indicated a distance of behavioural avoidance of attack sites of about 1.6 cm for the bark beetle.
Density maps of different local radii are also shown for Norway spruce trees killed by the bark beetle Ips typographus near Trebon, Czechoslovakia. Density maps using different local radii and density increments are presented for aggregated patterns of fallen Scots pine shoots, Pinus sylvestris, infested by Tomicus minor bark beetles in southern Sweden.
A method is presented for statistical comparison of randomly-generated spatial point data with natural data by using Chi-square analysis of the histograms of differently, coloured grid cells.

Visualization and analysis of the spatial distributions of individuals or groups of organisms in nature is basic to ecological research. A common method of spatial analysis to determine whether organisms are distributed more uniformly than random, at random, or in an aggregated pattern involves sample plots (Greig-Smith 1952, Morisita 1965, Lloyd 1967, Goodall and West 1979, Taylor 1984). These techniques rely on comparing the variance in the number of objects within sample plots in an area to determine the degree of "clumping"; a high variance indicates clumping (as some plots have low numbers and others high numbers) while a low variance indicates a uniform pattern. In contrast, "plotless" techniques rely on point-to-organism or organism-to-organism (nearest neighbour analysis) to detect the degree of clumping or dispersion. A larger than expected distance indicates over-dispersion while a smaller than expected distance (than random) indicates aggregations (Clark and Evans 1954, Thompson 1956, Pielou 1959). The above methods reduce two-dimensional data to an index, which is useful for determining the degree of dispersion, but information about local density and spatial orientation is lost.

Maps showing the locations of organisms reveal both their density and spatial relationships. The most widely used previous method for presenting these maps derived from Ashby and Pidgeon (1942) where the area is divided into grid cells that are allocated colours depending on the number of points within a cell. This method is wholly dependent on the grid resolution; and attempting to map the density contours results in discontinuous lines due to the integral values within grid cells. Several newer methods exist for contour mapping of densities, not all of them easily implemented by ecologists on computer. These include trend surface analysis, local weighted averaging, Fourier series modelling, spline, moving average, kriging, and kernel estimators (Legendre and Fortin 1989). Cox (1979) provides a method related to the k-nearest neighhour estimator (Diggle 1981) that produces contour maps (as traced by hand). Qualitatively better results using a kernel method are shown by Diggle (1981). Trend surface maps of the sixth order polynomial yield contour maps but these appear less detailed than maps obtained by kriging techniques (Legendre and Fortin 1989). In the above techniques the contour values obtained do not correspond to real local densities. Also the contour maps must be further analysed to indicate whether the points are distributed at random or with some other pattern.

A method is presented here, for use on personal computers, that displays spatial points (x, y coordinates) and uses them to colour a map of rectangular patches (grid cells) in a contoured pattern corresponding to the density ot points in the immediate vicinity of each patch. Both the density levels corresponding to various colours (or shadings on laser printer paper) and the radius of the vicinity for density calculations can be varied. Independent of these, the number of grid lines along the x- or v-axes of the map also can be varied up to 120. The density mapping method also directly yields histograms of coloured cells for use in a statistical analysis of spatial point distributions. Examples of the density mapping method are given for bark beetle attack points by Pityogenes chalcographus (L.). on bark of Norway spruce, Picea abies (L.) Karst., and for spruce trees killed by another bark beetle, Ips typographus (L.). These two species are termed 'aggressive' in that they must collectively kill the host tree for reproduction to proceed (Byers 1989). Forest species diversity and patch dynamics in Europe (Prentice and Leemans 1990) are significantly affected by these bark beetles. The density mapping method is also applied to distributions of Scots pine shoots, Pinus sylvestris L., infested by another bark beetle, Tomicus minor (Hartig), laying on the forest floor. T. minor and the sympatric species, T. piniperda (L.), which also infests shoots, cause significant growth reduction in Scots pine, but the beetles do not usually attack and kill standing trees, rather they feed and reproduce in fallen, storm-damaged trees.
Norway spruce bark scraped on left to reveal entrance holes of Ips typographus (larger holes) spaced apart from each other and Pityogenes chalcographus (smaller holes). Bark on left is also infested but the holes are under frass or small flakes of bark.


Methods

Computer program and algorithms
The program requires QuickBASIC 4.0) (Microsoft Corp.) to edit the source code (Appendix 1A-1C), while a compiled version operates from the DOS command line. The program's graphics automatically adjusts to the highest possible resolution of either the EGA (enhanced graphic, 640 x 350 pixels) or VGA (vector graphic array, 640 x 480 pixels) video displays. Automatic, but approximate, scaling of the map for the video display is performed, while the scaling for an optional laser-print copy is exact. Thus, only EGA and/or VGA monitors in colour or monochrome modes can be used. For printed output, which is optional, three laser printer drivers are included in the program for use with either PCL (Hewlett-Packard), EXPRESS (Kyocera Corp.), or PostScript (Adobe Corp.) command languages and compatible laser printers (Appendix 1C).

To use the program as outlined in Fig. 1, one begins by entering x, y coordinates of data into a computer file for future retrieval (Fig. 1B).
Fig. 1. Flow diagram of the computer program for displaying maps of spatial data and contour densities (see text for details).

It is also possible to create files of randomly selected x, y coordinates for any number of points in any size area for use in statistical comparison of histograms, as will be explained subsequently. In the next steps (Fig. 1C-D), assuming grid values have not been calculated earlier, one enters the number of grid lines desired for the largest side of the rectangular sample area. The grid lines for the smaller side are calculated proportionally, as are other scaling factors. The radius (R) of the circular area, within which local density is calculated, is determined by:

R = J(ED) (1)

where J is an arbitrary multiplier of the expected average nearest neighbour distance (ED), calculated by assuming that the points are distributed at random (Clark and Evans 1954):

ED = 0.5 SQRT(N/AREA) (2)

where N is the number of points and AREA is the surface area.

The x, y coordinates and lengths of the area's sides are loaded from a file. Then for each intersection of vertical and horizontal grid lines, the program counts the number of data points within a distance of R (Fig. 1E). These resulting grid values represent the local densities about each grid line intersection. The density for each grid cell is then described as the average of the grid line intersection densities of the respective four cell corners (Fig 1F). This average density, rather than a single value from the center of the grid cell, is used to smooth transitions in order to avoid broken or incomplete contours. The results of the calculation of grid values are saved in a file for fast retrieval when one only wants to adjust the histogram class interval (D). These grid cells (Fig. 1G) are then coloured or shaded on a map based on their membership within a histogram of density classes (k).

Thus, the radius of the local density area can be adjusted in order to coincide with ecological knowledge regarding the attributes of the species considered. In addition, the histogram of density class increments (D) can be varied to yield appropriate variation in the colour patterns based upon the aesthetics and experience of the investigator. This can be done by merely adjusting D, without the need to recalculate grid values. Different coloured cells represent different densities d of known value:

d = Dk/(3.141593((ED)J)2) (3)

where D, k, ED, and J are given above.

Natural and simulated point patterns
The pattern of attacks of male Pityogenes chalcographus on Norway spruce, P. abies, in Grib skov, Denmark, was recorded by overlaying a plastic sheet on the bark and marking it with ink (25 May 1987). The marks were then measured for x and y coordinates. An average nearest neighbour distance analysis was done on the attack distribution (Clark and Evans 1954, Thompson 1956) with a previously described computer program (Byers 1984). A minimum allowed distance analysis (MAD) was also performed on the attacks (Byers 1984). A simulated placement of 179 attacks at random was done by the computer program for comparison with the natural attacks above. Contour maps of different grid line numbers, local area radii (JxED), and density class increments (D) were compared to evaluate the method as performed by the program.

The pattern of fallen pine shoots of Scots pine, P. sylvestris, infested by T. minor near Veberöd, Sweden, was obtained by placing a string grid (2 x 3 m cells) over the area and measuring x, y coordinates within each cell (10 April 1989). The x,y coordinates for attacked trees of Norway spruce near Trebon, Czechoslovakia, by I. typographus (30 May 1987) were provided by Schlyter (unpubl.).

Comparison of grid cell density histograms

The program generates a histogram based on the numbers of differently coloured grid cells obtained for a particular set of data at a specific local radius and density class increment. Comparison of different histograms is useful to determine whether two spatial patterns (at the same density) are significantly different. For example, the frequency histogram of coloured grid cells for a random placement of 179 points calculated using a radius of 2 times the expected average nearest neighbour distance (ED) and a class interval of D = 1.5 was compared to a similarly constructed histogram for bark attacks of P. chalcographus (data from Fig. 2) using a Chi-square test. The density histogram for the random points was also compared by Chi-square with a histogram from a simulated aggregated pattern at the same overall density. This latter pattern was simulated by placing at random 29 groups of 6 points plus five additional points (179 points total) inside a 30 x 45 cm area. The points within each group were placed at random inside 5 x 5 cm areas completely contained in the larger area.

Results Natural and simulated point patterns

In Fig. 2 the map of density levels for 179 attacks by male P. chalcographus that occurred in a rather uniform pattern is shown.
Fig. 2. Upper map contains five density levels calculated from 179 natural attacks of male Pityogenes chalcographus in a 30 x 45 cm bark area of Norway spruce. The lower map has seven density levels based on random placement of 179 points. In both maps, the radius of local density areas was made twice the nearest neighhour distance expected from a random distribution at the same overall density. The shaded levels were based on increasing density steps of 0.063 cm = (or D = 1.5 points per local area) in both maps.
Identical parameters (39 x 25 grid cells; local radius of twice the ED; D = 1.5; 179 points in 45 x 30 cm area) were used to construct the density map for P. chalcographus and for the randomly distributed points (Fig. 2). The ED for a random pattern at this density is expected to be 1.37 cm (Clark and Evans 1954). The average nearest neighhour distance (NN) for attacks of P chalcographus was larger (1.99 ± 0.1 cm, ±95% C.L.) as analysed by a computer program (Byers 1984) and gave a ratio of NN/ED of 1.45 which was significantly different from 1 (P < 0.001, Clark and Evans 1954). The average distances for the second to fourth nearest attack neighbours were also larger than those expected from a random pattern (Thompson 1956). This indicates that male P. chalcographus avoid competition by a behavioural mechanism of attack spacing as was previously shown for males of another bark beetle, I. typographus (Byers 1984).

The minimum allowed distance (MAD) method uses quadratic regression to compare a curve of NNs from computer simulated patterns (random to overly dispersed) with the NN for a population to obtain a MAD that individuals may respect in nature (Byers 1984). This estimate of a MAD was relatively independent of density in I. typographus, indicating an inherent spacing behaviour characteristic of the species. The same analysis was performed on the data of P. chalcographus (Fig. 2) and gave a MAD of 1.6±0.03 cm (±95% C.L., n = 6). The MAD for the smaller sized P. chalcographus (2 mm long) is less than the MAD (2.5 cm) for the larger I. typographus (6 mm long). This is consistent with the smaller space requirements of P. chalcographus, due to its smaller size, in the two-dimensional phloem habitat in Norway spruce, the host of both species.

The effect of changing the length of the radius about each grid line intersection when calculating local densities as well as the density class increment (to yield eight colour levels) can be seen in the contour density maps in Fig. 3.
Fig. 3. The effect of using different radii for the local density areas is shown for fallen pine shoots damaged by Tomicus minor in an 8 x 15 m forest area of Scots pine. The upper map was based on a local radius of four times the expected nearest neighhour distance (ED) and density level increments ot 0.295 m-2. The middle map used a radius of 2 x ED and density increments of 0.429 m-2, while the lower map used a radius of ED and increments of 0.859 m-2. A fallen Scots pine brood tree (abandoned galleries of T. minor) lay along the left edge of the map area.
Each of the three maps reports densities of T. minor infested Scots pine shoots lying on the ground based on a different estimate of the importance of interactions by nearby organisms. The use of a larger as opposed to a smaller distance means that one considers interactions to be significant over a larger distance. The choice of the more appropriate map among the three is thus affected by the objectives for illustrating the relationships among the organisms. The effect of changing only the local radii in the density map is shown for Norway spruce trees killed by I. typographus (Fig. 4).
Fig. 4. The left map shows the mosaic pattern of densities of Norway spruce trees killed by Ips typographus based on increments of (0.139 m-2 calculated at a local area radius of two times the expected nearest neighbour distance (ED). The same data is represented in the right map but using density increments of 0.026 m-2 and a local area radius of ED. The two maps have the same 20 x 60 m area, with the forest-clearcut edge on the right side of each map (data from Schlyter et al., unpubl.).

Comparison of grid cell density histograms

One advantage of grid cell contour mapping of densities over some related methods is that statistical comparisons of spatial patterns are possible. As can be seen in Figs 2-4, the maps consist of grid cells of various "colours" representing density ranges corresponding to classes in a histogram. In a 40 x 26 grid line map there are 39 x 25 = 975 grid cells which can be categorized into a histogram that can be compared to another histogram obtained from another distribution of 97.5 grid cells. In Fig. 5, the histogram of grid cell densities for the attack pattern of P. chalcographus (Fig. 2) is compared to histograms of the random pattern (Fig. 2) and an aggregated pattern of 29 randomly placed clumps.
Fig. 5. Histograms of local density grid cell categories based on a radius of two times the expected average nearest neighbour distance (ED) and density increments of 0.063 cm-2 (D = 1.5 per local area). The histogram for P. chalcographus attacks and random points are from the grid cells of different densities shown in Fig. 2. Chi-square goodness of fit showed that the distribution of differently shaded grid cells obtained from the random pattern was significantly different from both the distributions obtained from the attacks (P < 0.001 ) and from the simulated aggregations (P < 0.001).
As expected, the histogram from the more uniform pattern of attacks has a leptokurtic distribution compared to a normal distribution for the histogram from the random pattern. The frequency histograms of these two patterns were significantly different (P < 0.001, X2). Comparisons of several histograms from several different random point distributions, constructed as above, indicated that they were not different from an averaged histogram of three such distributions.

As can be seen from Table 1, several grid cell frequency histograms using different R and D values for the uniform pattern compared to an average of three random patterns were in all cases significantly different, while the random pattern in Fig. 2 was not different.
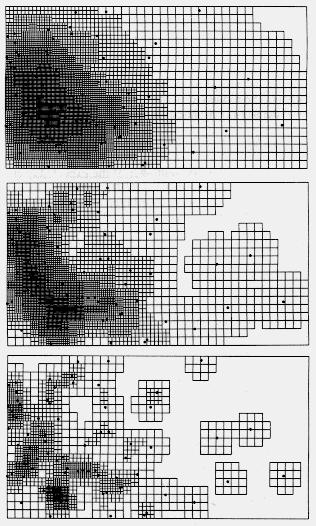
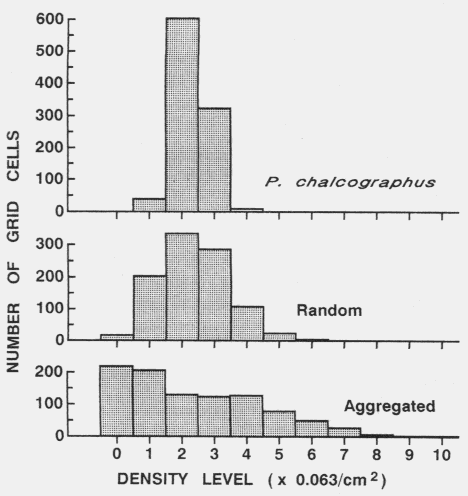
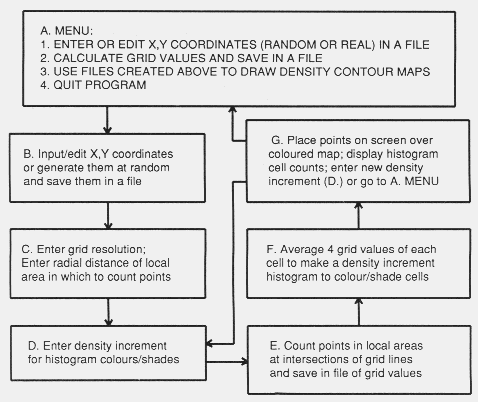
Table 1. P values (and degrees of freedom) for Chi-square comparisons of grid cell colour frequency histograms from contour maps of Pityogenes chalcographus attacks or random points (data in Fig. 2) with an average histogram from three random data sets. Comparisons were made between histograms from maps constructed at various D (density class increments) and R (expected average nearest neighhour distance) values, while densities and grid parameters were identical.
P values for Chi-square (df)
D = 1D = 2D = 3
Random points
R = 10.64(3)0.54(2)0.27(1)
R = 20.80(8)0.41(4)0.46(3)
R = 30.28(11)0.17(6)0.08(4)
P. chalcographus
R = 1< 0.001(2)< 0.001(1)< 0.001(1)
R = 2< 0.001(4)< 0.001(2)< 0.001(1)
R = 3< 0.001(6)< 0.001(3)< 0.001(2)

Thus, it makes little difference which local radius or density increment is used, unless the density increment is so large as to include only one colour. The aggregated pattern was also significantly different (P < 0.001) from the random pattern. It is suggested that a frequency histogram for a random point pattern be constructed from an average of at least three data sets each with parameters of density, grid lines, R and D values corresponding appropriately to that used for the map of the natural data.

Discussion

Males of P chalcographus produce a two-component pheromone that is used by responding individuals of both sexes to locate an infested Norway spruce tree (Byers et al. 1988, 1990). The female, unlike the male, has an interest in orienting directly to an entrance hole in the bark since up to six females reside with each male in their gallery. The host-plant monoterpenes, alpha-pinene, (B-pinene, and 3-carene, are also used by beetles to locate and enter the attack holes (Byers et al. 1988). P. chalcographus males avoid attacking too close to established sites as shown by the nearest neighbour analysis, the minimum allowed distance (MAD) analysis, and the density map in Fig. 2. Spacing of attacks has been shown for some other bark beetles (e.g. T. piniperda and I. typographus) and has been attributed to an avoidance of competition for the phloem layer (Byers 1984). However, the mechanisms responsible for spacing apart of the attacks have not been revealed.

One theory is that bark beetles use acoustic stridulation to space apart attacks (Rudinsky and Michael 1973), although P. chalcographus is not known to stridulate. Another theory is that bark surface irregularities constrain the pattern of attacks (Safranyik and Vithayasai 1971). This possibility, however, is small since the Norway spruce bark in the region of the sample (Fig. 2) was `smooth' with a uniform granularity that should not limit the distribution of desirable attack sites. An olfactory mechanism may be used by male P. chalcographus to avoid boring too close to others since males are less attracted than females to progressively higher concentrations of synthetic pheromone release (Byers et al. 1988). There are no known repellent pheromone or host components which might serve to space attacks as found in other bark beetles (Byers 1983, Byers et al. 1989). Frass piles resulting from excavated host tissue (outer bark and phloem tissue) and fecael pellets are clearly stimulatory to females (pers. obs.) and thus could be repellent to males as part of a spacing mechanisms.

The pine shoot beetles, T. minor and T. piniperda, concentrate en masse on fallen storm-damaged Scots pine in the spring in response to the monoterpenes, alpha-pinene, 3-carene, and terpinolene volatilizing from wound oleoresin (Byers et al. 1985, Lanne et al. 1987). This olfactory mechanism serves both in host-plant recognition and in the determination of host susceptibility to attack and colonization (Byers et al. 1985). However, only T. minor has been shown to aggregate on hosts in response to a pheromone (Lanne et al. 1987). Following reproduction in the host-tree, the young adults fly to the crowns of surrounding Scots pine trees where they seek shoots in which to feed for the remainder of the summer (Långström 1983). The infested shoots then fall from the trees during winter storms. It is clear from the maps (Fig. 3) that T. minor flies only some metres after emergence from the brood tree in July, in contrast to much larger distances expected during the spring dispersal and brood-tree location flight in April. This aggregated pattern of pine shoots is consistent with the findings of Forsse (1989). He showed that the flight durations of T. minor and T. piniperda on flight mills after their emergence from brood trees in summer were much shorter than when they seek hosts in which to breed the next spring. The results indicate that estimates of populations of Tomicus beetles that are based on pine shoot densities will require more intensive sampling than if the patterns had been uniformly random throughout the forest.

Both sexes of Ips typographus aggregate in response to a two-component pheromone blend produced by the males during their boring into Norway spruce (Bakke et al. 1977, Birgersson et al. 1984, Schlyter et al. 1987a,b). Norway spruce trees may be colonized in groups at higher insect populations through a process whereby some beetles by chance land on nearby trees instead of focusing to the attractant source. The attacking male is more likely to deviate from a direct path to the pheromone source than is the female as shown in both I. paraconfusus Lanier (Byers 1983) and I. typographus (Schlyter et al. 1987a,b). Beetles may attack more trees on the edge of the clearcut (Fig. 4) because temperatures here are warmer for longer periods than inside the forest (Byers and Löfqvist 1989). A second possibility is that beetles prefer the edges of clearcuts since they are not hindered during flight. It also may be assumed that trees on the edges are more susceptible to attack due to climatic stress imposed by their recent exposure (Christiansen et al. 1987).

The density mapping method presented here is useful for exploratory illustration of spatial distributions of organisms, shows densities with relative and absolute components, and allows for a sensitive statistical comparison of uniform, random, and aggregated patterns. Contour maps of density have been constructed from actual counts in grid cells (e.g. Ashby and Pidgeon 1942, Kitajima and Augspurger 1989) but the resulting densities were entirely dependent on the original grid placement and size. Also, the contouring techniques were not presented. Most contour methods previously used have relied on a fixed and arbitrary grid placement to calculate densities, while the method here uses variable and symmetrical radial areas for density calculation. Although the present method is still influenced by the grid resolution, the resolution can be varied independently of the areas of density measurement. The present method allows spatial density patterns to be viewed in alternative ways due to the ability to independently change (1) grid resolution, (2) local area radii (R), which allows one to "smooth" density contours, and (3) the number of different "colours" by varying the density increment (D).

Cox (1979) used an arbitrary set of parameters, including various weights given to successive nearest neighbour distances from grid cell corner points to calculate values of relative density for use in a contour mapping program (SYMAP). He acknowledged that the choice of the parameters "reflects one's ideas or needs of what constitutes a dense or sparse region", a concept promoted here as well. The method presented here is different, however, in that actual densities are calculated in regions defined by an arbitrary radius (some multiple of the expected nearest neighbour distance) from the grid cell corners. The method of Cox (1979) used SYMAP to produce the contours but these had to be traced by hand and no facilities for colours or shades are evident.

The methods of trend surface analysis, kriging, and kernel estimators (Silverman 1981, Diggle 1981, Legendre and Fortin 1989) also give results qualitatively similar to the method here. However, they are less flexible in that only one map is constructed based on a specific kernel or polynomial. The harmonic mean of a point distribution has been used to draw contour maps of an animal's home range (Dixon and Chapman 1980, Spencer and Barrett 1984, Ostfeld 1986). However, density calculations are not done and no attempt is made to analyse the uniformity of the point distribution since this question is not relevant to the description of the home range. Powell (1990) presents spatial maps of seedlings and adult plants of diffuse knapweed, Centaurea diffusa, which show differences in densities along a rectangular transect. The density trace method of Wegman (1972) clearly indicated differences in density, although this method depends on the angle of movement during the analysis. The contour mapping program described here could have been used to analyse smaller regions of the transect.

The density contouring method and computer program should aid the visualization of spatial point densities and patterns, aid in determining differences in point patterns, and aid in production of camera-ready figures (as produced here) for publication. The source code of the program is listed in the Appendix and a compiled version is available from the author (send a formatted disk and return mailer).

Acknowledgements - Funding for the work was contributed by the Swedish Forest and Agricultural Research Agency (SJFR). I also thank F. Schlyter for collection of the data on the Norway spruce trees killed by Ips typographus.

John A. Byers

Department of Animal Ecology, Lund University, SE-223 62 Lund, Sweden

Present address:


References
Ashby, E. and Pidgeon, I. M. 1942. A new quantitative method of analysis of plant communities. - Aust. J. Sci. 5: 19-20.

Bakke, A.. Froyan, P. and Skattebol, L. 1977. Field response to a new pheromonal compound isolated from Ips typographus. - Naturwissenschaften 64: 98.

Birgersson, G., Schlyter, F., Löfqvist, J. and Bergström, G. 1984. Quantitative variation of pheromone components in the spruce bark beetle Ips typographus from different attack phases. - J. Chem. Ecol. 10: 1029-1055.

Byers, J. A. 1983. Sex-specific responses to aggregation pheromone: Regulation of colonization density by the bark beetle, Ips paraconfusus - J. Chem. Ecol. 9: 129-142.

Byers, J.A. 1984. Nearest neighbor analysis and simulation of distribution patterns indicates an attack spacing mechanism in the bark beetle, Ips typographus, (Coleoptera: Scolytidae). - Environ. Entomol. 13: 1191-1200.

Byers, J.A. 1989. Chemical ecology of bark beetles. - Experientia 45: 271-283.

Byers, J.A. and Löfqvist, J. 1989. Flight initiation and survival in the bark beetle Ips typographus during the spring dispersal. - Holarct. Ecol. 12: 432-440.

Byers, J.A., Lanne, B. S., Schlyter, F., Löfqvist, J. and Bergström, G. 1985. Olfactory recognition of host-tree susceptibility by pine shoot beetles. - Naturwissenschaften 72: 324-326.

Byers, J.A., Birgersson, G., Löfqvist, J. and Bergström, G. 1988. Synergistic pheromones and monoterpenes enable aggregation and host recognition by a bark beetle. - Naturwissenschaften 75: 153-155.

Byers, J.A., Lanne, B. S. and Löfqvist, J. 1989. Host-tree unsuitability recognized by pine shoot beetles in flight. - Experientia 45: 489-492.

Byers, J.A., Birgersson, G., Löfqvist, J., Appelgren, M. and Bergström, G. 1990. Isolation of pheromone synergists of bark beetle, Pityogenes chalcographus, from complex insect-plant odors by fractionation and subtractive-combination bioassay. - J. Chem. Ecol. 16: 861-876.

Christiansen, E., Waring, R. H. and Berryman, A. A. 1987. Resistance of conifers to bark beetle attack: Searching for general relationships. - For. Ecol. Manage. 22: 89-106.

Clark, P. J. and Evans, F. C. 1954. Distance to nearest neighbour as a measure of spatial relationships in populations. - Ecology 35: 445-453.

Cox, T. F. 1979. A method for mapping the dense and sparse regions of a forest stand. - Appl. Statist. 28: 14-19.

Diggle, P. J. 1981. Some graphical methods in the analysis of spatial point patterns. - In: Barnet, V. (ed.), Interpreting multivariate data. John Wiley and Sons, New York, pp. 55-73.

Dixon, K. R. and Chapman, J. A. 1980. Harmonic mean measure of animal activity areas. - Ecology 61: 1044-1044.

Forsse, E. 1989. Migration in bark beetles with special reference to the spruce bark beetle Ips typographus. - Ph.D. Thesis (paper V), Swedish Agric. Univ., Uppsala.

Goodall, D. W. and West, N. E. 1979. A comparison of techniques for assessing dispersion patterns. - Vegetatio 40: 15-27.

Greig-Smith, P. 1952. The use of random and contiguous quadrats in the study of the structure of plant communities. - Ann. Bot. 16: 293-316.

Kitajima, K. and Augspurger, C. K. 1989. Seed and seedling ecology of a monocarpic tropical tree, Tachigalia versicolor. - Ecology 70: 1102-1114.

Långström, B. 1983. Life cycles and shoot-feeding of the pine shoot beetles. - Stud. Forest. Suec. 163: 1-29.

Lanne, B. S., Schlyter, F., Byers, J. A., Löfqvist, J., Leufvén, A., Bergström, G., Van Der Pers, J. N. C., Unelius, R., Baeckström, P. and Norin, T. I987. Differences in attraction to semiochemicals present in sympatric pine shoot beetles, Tomicus minor and T. piniperda. - J. Chem. Ecol. 13: 1045-1067.

Legendre, P. and Fortin, M. J. 1989. Spatial pattern and ecological analysis. - Vegetatio 80: 107-138.

Lloyd, M. 1967. Mean crowding. - J. Anim. Ecol. 36: 1-30.

Morisita, M. 1965. A revision of the methods for estimating population values of the index of dispersion in the I8, - method. - Res. Popul. Ecol. 7: 126-128.

Ostfeld, R. S. 1986. Territoriality and mating system of California voles. - J. Anim. Ecol. 55: 691-706.

Pielou, E. C. 1959. The use of point-to-point distances in the study of the pattern of plant populations. - J. Ecol. 47: 607-613.

Powell, R. D. 1990. The role of spatial pattern in the population biology of Centaurea diffusa. - J. Ecol. 78: 374-388.

Prentice, I. C. and Leemans, R. 1990. Pattern and process and the dynamics of forest structure: A simulation approach. - J. Ecol. 78: 340-355.

Rudinsky, J. A. and Michael, R. R. 1973. Sound production in Scolytidae: stridulation by female Dendroctonus beetles. - J. Insect Physiol. 19: 689-705.

Safranyik, L. and Vithayasai, C. 1971. Some characteristics of the spatial arrangement of attacks by the mountain pine beetle, Dendroctonus ponderosae (Coleoptera: Scolytidae), on lodgepole pine. - Can. Entomol. 103: 1607-1625.

Schlyter, F., Byers, J. A. and Löfqvist, J. 1987a. Attraction to pheromone sources of different quantity, quality and spacing: Density-regulation mechanisms in the bark beetle Ips typographus. - J. Chem. Ecol. 13: 1503-1523.

Schlyter, F., Löfqvist, J. and Byers, J. A. 1987b. Behavioural sequence in the attraction of the bark beetle Ips typographus to pheromone sources. - Physiol. Entomol. 12: 185-196.

Silverman, B. W. 1981. Density estimation for univariate and bivariate data. -In: Barnett, V. (ed.), Interpreting multivariate data. John Wiley and Sons, New York, pp. 37-53.

Spencer, W. D. and Barrett, R. H. 1984. An evaluation of the harmonic mean measure for defining carnivore activity areas. - Acta Zool. Fenn. 171: 255-259.

Taylor, L. R. 1984. Assessing and interpreting the spatial distributions of insect populations. - Annu. Rev. Entomol. 29: 321-357.

Thompson, H. R. 1956. Distribution of distance to nth neighbour in a population of randomly distributed individuals. - Ecology 37: 391-394.

Wegman, E. J. 1972. Non-parametric probability density estimation. I. A summary of available methods. - Technometrics 14: 533-546.



Appendix 1A. QuickBASIC listing of main part of contour density mapping program.

2 ON ERROR GOTO 4: GOTO 8: '$DYNAMIC
4 SCREEN 0: COLOR 15: CLS : IF ERR = 5 AND ERL = 10 THEN RESUME 12
6 PRINT "BASIC ERROR ="; ERR; " ON LINE ="; ERL; " (APPLICABLE ONLY FOR BASIC SOURCE CODE)": END
8 DEFINT C, G, M-N, W, Z: DIM X(5000), Y(5000), G(120, 120), C(20)
10 WIDTH 80: IYL = 480: YL = IYL: DEF SEG = 0: SCREEN 12: COLOR 11: CLS : GOTO 16
12 WIDTH 80: IYL = 350: DEF SEG = 0: SCREEN 9
14 CLOSE : COLOR 11: CLS : YL = IYL: QW = 0
16 LOCATE 2, 8: PRINT "CONTOUR MAPPING OF DENSITIES OF ORGANISMS: USING GRID OF"
18 LOCATE 3, 14: PRINT "20X20 UP TO 120X120 in ANY RECTANGULAR AREA"
20 LOCATE 4, 20: PRINT "(C) 1990 by John A. Byers": COLOR 15: LOCATE 6, 4: PRINT "PRESS NUMBER BELOW:"
22 COLOR 13: FOR W = 8 TO 14 STEP 2: LOCATE W, 1: PRINT INT((W - 6) / 2): NEXT: COLOR 15
24 LOCATE 8, 4: PRINT "ENTER OR EDIT X,Y COORDINATES (RANDOM OR REAL) AND SAVE IN A FILE"
26 LOCATE 10, 4: PRINT "CALCULATE GRID VALUES AND SAVE IN A FILE"
28 LOCATE 12, 4: PRINT "USE FILES CREATED IN #1 AND #2 ABOVE TO DRAW DENSITY CONTOUR MAPS"
30 LOCATE 14, 4: PRINT "QUIT PROGRAM"
32 Y$ = INKEY$: IF Y$ = "" THEN 32
34 IF Y$ = "1" THEN GOSUB 500: GOTO 14 ELSE IF Y$ = "2" THEN 42
36 IF Y$ = "3" THEN QW = 1: GOTO 42 ELSE IF Y$ = "4" THEN END ELSE SOUND 500, .2: GOTO 32
38 EN = 0: B = INSTR(Y$, E$): IF B < 2 OR B > 9 THEN EN = 1: SOUND 50, 1: PRINT "NAME MUST END IN "; E$
40 RETURN
42 OPEN "EXAMPLE.GRD" FOR RANDOM AS #1 LEN = 1: CLOSE #1: COLOR 15: FILES "*.COO"
44 COLOR 11: INPUT "ENTER the FILE NAME that has the X,Y COORDINATES (.COO)"; Y$: Y$ = UCASE$(Y$)
46 E$ = ".COO": GOSUB 38: IF EN = 1 THEN 44
48 A = 2: GOSUB 50: IF EN = 1 THEN 44 ELSE CO$ = Y$: GOTO 56
50 EN = 0: OPEN Y$ FOR RANDOM AS #A
52 IF LOF(A) = 0 THEN CLOSE #A: SOUND 50, 1: PRINT "FILE DOES NOT EXIST !": KILL Y$: EN = 1: RETURN
54 CLOSE #A: RETURN
56 COLOR 15: FILES "*.GRD": COLOR 11: IF QW = 0 THEN 62
58 INPUT "ENTER the FILE NAME that has the GRID VALUES (.GRD)"; Y$: Y$ = UCASE$(Y$)
60 E$ = ".GRD": GOSUB 38: IF EN = 1 THEN 62 ELSE A = 1: GOSUB 50: IF EN = 1 THEN 58 ELSE 70
62 INPUT "ENTER the FILE NAME to hold GRID VALUES (.GRD)"; Y$: Y$ = UCASE$(Y$)
64 E$ = ".GRD": GOSUB 38: IF EN = 1 THEN 62
66 OPEN Y$ FOR RANDOM AS #1: IF LOF(1) > 0 THEN SOUND 50, 1: GOTO 68 ELSE 70
68 INPUT "YOU HAVE THIS FILE ALREADY - OVERWRITE? y/n"; Q$: Q$ = UCASE$(Q$): IF Q$ <> "Y" THEN 14
70 CLOSE #1: GR$ = Y$: COLOR 15: IF QW = 1 THEN 78
72 INPUT "How many GRID POINTS per SIDE of AREA (ENTER 20 to 120)"; GN: D = 2
74 IF GN > 120 OR GN < 20 THEN SOUND 50, 2: GOTO 72
76 INPUT "MULTIPLYER of NEAREST NEIGHBOR DIST. for GRID POINT R (ENTER .1 to 4)"; J: GOTO 82
78 LS = 0: INPUT "ENTER 1 if you want LASER copy or HIT ENTER if not"; LS: IF LS = 1 THEN GOSUB 800
80 INPUT "ENTER DENSITY STEP VALUE? (.1 to 10 usually)"; D: M = 0: IF D = 0 THEN SOUND 50, 1: GOTO 80
82 IF LS <> 1 THEN LS = 0: GOTO 84 ELSE INPUT "ENTER 1 To See GRID LINES on LASER PRINTOUT"; GL
84 COLOR 1: CLS : IF QW = 0 THEN 86 ELSE OPEN GR$ FOR INPUT AS #1: INPUT #1, GN
86 XL = 540: OPEN CO$ FOR RANDOM AS #2 LEN = 32: REM LOAD FILE
88 FIELD #2, 6 AS J$, 13 AS A$, 13 AS B$: GET #2, 1: XA = VAL(A$): YA = VAL(B$): BP = 26
90 IF YA = XA THEN GX = GN: GY = GN: XC = XL / XA: YC = YL / YA ELSE GOTO 94
92 XS = XL - 1: YS = YL - 1: SCX = 16 / XA: SCY = SCX: GOTO 102
94 IF YA > XA THEN GY = GN: GX = INT(XA / YA * GN): YC = YL / YA ELSE GOTO 98
96 XS = XL * XA / YA: YS = YL - 1: XC = XL / YA: SCX = 16 / XA * (XA / YA): SCY = 16 / YA: GOTO 102
98 IF XA > YA THEN GX = GN: GY = INT(YA / XA * GN): XC = XL / XA: XS = XL - 1
100 YS = YL * YA / XA: YC = YL / XA: SCX = 16 / XA: SCY = 16 / YA * (YA / XA)
102 LE = 2: BY = 7: FOR W = 0 TO 20: C(W) = 0: NEXT: C = 1: NB = 0: REM conversion from real to screen
104 WHILE EOF(2) = 0: C = C + 1: GET #2, C: IF ASC(J$) > 0 THEN 106 ELSE 108
106 IF VAL(A$) > 0 OR VAL(B$) > 0 THEN NB = NB + 1: X(C - 1) = VAL(A$): Y(C - 1) = VAL(B$)
108 WEND: CLOSE #2: SX = XS / (GX - 1): SY = YS / (GY - 1): GOSUB 110: GOTO 118
110 FOR X = 0 TO XS + .1 STEP SX: LINE (X, YL - YS - 1)-(X, YL - 1): NEXT: FOR Y = 0 TO YS + .1 STEP SY
112 LINE (0, YL - (YS - Y + 1))-(XS, YL - (YS - Y + 1)): NEXT: RETURN
114 IF LS = 0 THEN RETURN ELSE DOTL = 1: PD = .04: IF LS = 1 THEN GOSUB 800
116 DOTL = 2: IF LS = 1 THEN GOSUB 800: RETURN ELSE RETURN
118 COLOR 15: GOSUB 120: ED = .5 / SQR(NB / (XA * YA)): IF QW = 0 THEN R = ED * J: GOTO 124 ELSE 148
120 FOR W = 1 TO NB: T = X(W) * XC: U = YL - Y(W) * YC: PSET (T, U): NEXT: IF FT = 1 THEN RETURN
122 IF LS = 0 THEN RETURN ELSE DOTL = 3: GOSUB 800: RETURN
124 REM calculate number real points within R (ED*J) to each grid point
126 FOR B = 0 TO XA + .1 STEP XA / (GX - 1): CX = CX + 1
128 FOR A = 0 TO YA + .1 STEP YA / (GY - 1): CY = CY + 1: TD% = 0
130 A$ = INKEY$: IF A$ = "" THEN 132 ELSE IF A$ = CHR$(27) THEN END
132 FOR N = 1 TO NB: IF X(N) > B + R OR X(N) < B - R THEN 138
134 IF Y(N) > A + R OR Y(N) < A - R THEN 138 ELSE X = B - X(N)
136 Y = A - Y(N): IF SQR(X * X + Y * Y) <= R THEN TD% = TD% + 1
138 NEXT: IF A = 0 THEN YL = IYL - 1 ELSE YL = IYL
140 G(CX, CY) = TD%: PSET (B * XC, YL - A * YC), 15: NEXT: CY = 0: NEXT
142 OPEN GR$ FOR OUTPUT AS #2: PRINT #2, GN: REM save grid values
144 FOR W = 1 TO GX: FOR Z = 1 TO GY: PRINT #2, G(W, Z); : NEXT: NEXT: PRINT #2, R, J: CLOSE #2
146 FOR W = 1 TO GX: FOR Z = 1 TO GY: G(W, Z) = 0: NEXT: NEXT
148 OPEN GR$ FOR INPUT AS #2: INPUT #2, GN: REM get grid values, R, J
150 FOR W = 1 TO GX: FOR Z = 1 TO GY: INPUT #2, G(W, Z): NEXT: NEXT
152 INPUT #2, R, J: CLOSE #2: TL = (GX - 1) * (GY - 1): COLOR 1: CLS : GOSUB 110
154 C = 0: VX = XA / (GX - 1) * SCX: VY = YA / (GY - 1) * SCY
156 FOR LL = D TO 12 * D STEP D: C = C + 1: REM Color according to D level
158 FOR W = 1 TO GX - 1: FOR Z = 1 TO GY - 1
160 AVD = (G(W, Z) + G(W + 1, Z) + G(W, Z + 1) + G(W + 1, Z + 1)) / 4
162 IF AVD <= LL AND AVD > LL - D + .0001 THEN 166
164 IF C = 1 AND AVD = 0 THEN C(0) = C(0) + 1: M = M + 1: GOTO 172 ELSE 172
166 C(C) = C(C) + 1: M = M + 1: A = ((((W - 1) * SX + 1) + (W * SX + 1)) / 2)
168 B = YL - ((((Z - 1) * SY + 1) + (Z * SY + 1)) / 2): PAINT (A, B), C, 1: IF LS = 0 THEN 172
170 DOTL = 4: GOSUB 800
172 NEXT: NEXT: NEXT: COLOR 15: IF GL > 0 THEN GOSUB 114
174 FT = 1: GOSUB 120: FT = 0
176 IF JB > 0 THEN A = GX: B = GY: GY = 2: GX = 2: GOSUB 114 ELSE 180
178 DOTL = 5: IF LS = 1 THEN GOSUB 800: GX = A: GY = B
180 CLOSE : V = (XS / 640) * 80 + 2: COLOR 15: LOCATE 1, V: PRINT "E.A.NNd="
182 LOCATE 2, V: PRINT ED: LOCATE 3, V: PRINT "Radius=": LOCATE 4, V: PRINT R
184 LOCATE 5, V: PRINT "#="; NB: LOCATE 6, V: PRINT GX - 1; "X"; GY - 1: LOCATE 7, V
186 PRINT "D="; D: LOCATE 8, V: PRINT "D. STEP=": LOCATE 9, V: PRINT "D/(R^2*"; CHR$(227); "="
188 LOCATE 10, V: PRINT USING "##.######"; D / (R ^ 2 * 3.14159): LOCATE 11, V: PRINT "#/D. STEP"
190 FOR W = 12 TO 24: LOCATE W, V: C = W - 12: PRINT C; : COLOR C: PRINT CHR$(219); : COLOR 15
192 PRINT C(W - 12); : NEXT: LOCATE 25, V: PRINT "<ENTER/Esc>";
194 A$ = INKEY$: IF A$ = "" THEN 194
196 IF A$ = CHR$(27) THEN CLEAR : GOTO 2 ELSE PRINT : QW = 1: JB = 0: GOTO 78


Appendix 1B. QuickBASIC listing of routines for entering x,y coordinates in contour density mapping program

500 REM ENTERING OF X,Y COORDINATES ROUTINES
502 OPEN "EXAMPLE.COO" FOR RANDOM AS #1 LEN = 1: CLOSE #1
504 FILES "*.COO": CV = 3: IF IYL = 480 THEN SI = 120 ELSE SI = 100
506 COLOR 11: INPUT "ENTER the FILE NAME to hold (or edit) X,Y COORDINATES (.COO)"; Y$: Y$ = UCASE$(Y$)
508 E$ = ".COO": GOSUB 510: IF EN = 1 THEN GOTO 506 ELSE GOTO 514
510 EN = 0: B = INSTR(Y$, E$): IF B < 2 OR B > 9 THEN EN = 1: SOUND 50, 1: PRINT "NAME MUST END IN "; E$
512 RETURN
514 COLOR 15: OPEN Y$ FOR RANDOM AS #1 LEN = 32: FIELD #1, 6 AS J$, 13 AS A$, 13 AS B$
516 CLS : GET #1, 1: PRINT "THE X-AXIS = "; A$; "THE Y-AXIS = "; B$
518 X = VAL(A$): Y = VAL(B$): IF X = 0 OR Y = 0 THEN GOTO 524
520 COLOR 11: INPUT "HIT <ENTER> IF OK OR TO EDIT ENTER 1"; Y$
522 IF Y$ = "1" THEN 524 ELSE 528
524 INPUT "ENTER X-AXIS LENGTH of AREA"; X: INPUT "ENTER Y-AXIS LENGTH of AREA"; Y: LSET A$ = STR$(X)
526 LSET B$ = STR$(Y): PUT #1, 1
528 INPUT "ENTER a NUMBER for RANDOM GEN. of X,Y COORD.; ELSE HIT <ENTER>"; R
530 CLS : A = 41: C = 2: B = 219: K = 15: IF R > 0 THEN GOTO 614
532 PRINT "ENTER X,Y DATA, OR "; : COLOR 14: PRINT "*"; : COLOR 15: PRINT " <ENTER> to EDIT/SAVE"
534 LINE (15, IYL - (IYL - SI))-(350 + 15, IYL - (IYL - SI)), 1
536 LINE (15, IYL - 1)-(350 + 15, IYL - 1), 1: LINE (15, IYL - (IYL - SI))-(15, IYL - 1), 1
538 LINE (350 + 15, IYL - (IYL - SI))-(350 + 15, IYL - 1), 1: COLOR 12
540 LOCATE 9, 50: PRINT "INSTRUCTIONS:": LOCATE 11, 50: PRINT "ENTER a X and then a Y value"
542 LOCATE 12, 50: PRINT "for the x,y point coordinates."
544 LOCATE 13, 50: PRINT "When done ENTER an asterisk "; : COLOR 14: PRINT "*": COLOR 12
546 LOCATE 15, 50: PRINT "Then you may either:": LOCATE 16, 50: PRINT "Press [Esc] to save data file;"
548 LOCATE 17, 50: PRINT "Press [Enter] to REedit x,y's;"
550 LOCATE 18, 50: PRINT "Press [Delete] to delete OR"
552 LOCATE 19, 50: PRINT "[Insert] to insert x,y data."
554 LOCATE 20, 50: PRINT "Press ["; CHR$(24); CHR$(25); "] to move up or down"
556 LOCATE 21, 50: PRINT "through the x,y data list.": COLOR 15
558 LOCATE 7, 2: PRINT STRING$(79, 32); : LOCATE 7, 2: PRINT C - 1; "INPUT X";
560 INPUT X$: IF X$ = "*" THEN C = C - 1: GOTO 568
562 IF X$ <> "0" AND VAL(X$) = 0 THEN SOUND 500, .3: GOTO 558
564 LOCATE 7, 25: INPUT "INPUT Y"; Y$: LOCATE 7, 25: IF Y$ = "*" THEN C = C - 1: GOTO 568
566 IF Y$ <> "0" AND VAL(Y$) = 0 THEN SOUND 500, .3: PRINT STRING$(54, 32); : GOTO 564 ELSE 598
568 LOCATE 7, 2: PRINT "PRESS ["; CHR$(24); "]["; CHR$(25); "]; <ENTER> to EDIT; ";
570 PRINT "[Delete] or [Insert]; [Esc] to SAVE"; : IF CV > 5 THEN M = 6 ELSE M = CV + 1
572 IF CV > MJ THEN LOCATE M - 1, 33: PRINT STRING$(28, 32)
574 IF CV < MJ AND CV < 5 THEN LOCATE M + 1, 33: PRINT STRING$(28, 32)
576 MJ = CV: LOCATE M, 33: COLOR 12: PRINT CHR$(27); : COLOR 15: PRINT " NUMBER TO EDIT OR DELETE"
578 T$ = INKEY$: IF T$ = "" THEN GOTO 578 ELSE LOCATE M, 33: PRINT STRING$(28, 32)
580 IF T$ = CHR$(27) THEN RETURN ELSE IF RIGHT$(T$, 1) = "R" THEN JG = C: GOTO 638
582 IF RIGHT$(T$, 1) = "S" THEN K = 0: GOSUB 612: JG = C: GOSUB 634: GOTO 596
584 IF RIGHT$(T$, 1) = "H" AND C = W - 1 THEN W = 0: GOTO 596
586 IF RIGHT$(T$, 1) = "P" AND C = 2 AND K = 0 THEN K = 15: C = C - 1: GOSUB 612
588 IF RIGHT$(T$, 1) = "H" THEN K = 0: GOSUB 612: C = C - 1: K = 15: GOTO 594
590 IF RIGHT$(T$, 1) = "P" THEN C = C + 1: K = 15: GET #1, C: GOSUB 626: GOTO 596
592 LOCATE 6, 2: PRINT STRING$(33, 32): IF T$ = CHR$(13) THEN GOTO 628 ELSE GOTO 568
594 IF C < 2 THEN K = 0: C = 2: GOSUB 612
596 GET #1, C: CV = C: GOSUB 604: GOTO 630
598 IF VAL(X$) > X OR VAL(Y$) > Y THEN GOTO 632 ELSE GET #1, C: K = 0: GOSUB 612: K = 15
600 LSET J$ = STR$(C - 1): LSET A$ = X$: LSET B$ = Y$: PUT #1, C: C = C + 1
602 LOCATE 6, 2: PRINT STRING$(33, 32): CV = C - 1: GET #1, C - 1: GOSUB 604: GOTO 558
604 FOR T = 0 TO 4: IF CV - T < 1 THEN EXIT FOR
606 NEXT
608 FOR M = 2 TO 4: LOCATE M + 2, 1: PRINT STRING$(28, 32): NEXT: LOCATE 2, 1
610 FOR MK = CV - (T - 1) TO CV: GET #1, MK: PRINT J$; A$; B$: NEXT: POKE 1050, PEEK(1052)
612 CIRCLE (VAL(A$) / X * 350 + 15, IYL - VAL(B$) / Y * (IYL - SI)), 1, K: RETURN
614 PRINT "WHEN ADDING GENERATED X,Y COORDINATES IT IS BEST TO START WITH"
616 PRINT "A NEW FILE THAT DOES NOT CONTAIN ANY PREVIOUSLY GENERATED DATA."
618 INPUT "HOW MANY X,Y PAIRS DO YOU WANT"; N: PRINT "WAIT...": A = RND(-R)
620 FOR C = 2 TO N + 1: J = RND * X: A = RND: B = RND * Y: K = 15
622 LSET J$ = STR$(C - 1): LSET A$ = STR$(J): LSET B$ = STR$(B): PUT #1, C
624 GOSUB 612: NEXT: RETURN
626 IF ASC(J$) = 0 THEN W = C: RETURN ELSE W = 0: RETURN
628 IF C = W - 1 THEN C = W: GOTO 558 ELSE GOTO 558
630 IF C = W THEN C = C - 1: GOTO 568 ELSE GOTO 568: REM C=C-1
632 LOCATE 6, 2: PRINT "X OR Y VALUE OUT OF RANGE": SOUND 50, 1: GOTO 558
634 GET #1, JG + 1: IF VAL(J$) = 0 THEN RETURN ELSE LSET J$ = STR$(JG - 1): PUT #1, JG: REM DELETE
636 JG = JG + 1: LSET J$ = "": LSET A$ = "": LSET B$ = "": PUT #1, JG: GOTO 634
638 GET #1, JG: IF VAL(J$) = 0 THEN 640 ELSE JG = JG + 1: GOTO 638: REM insert
640 FOR JK = JG - 1 TO C STEP -1: GET #1, JK: LSET J$ = STR$(JK): PUT #1, JK + 1: NEXT: GOTO 596


Appendix 1A. QuickBASIC listing of routines for laser printing of contour density maps

800 REM LASER PRINTER SUBROUTINES
802 IF JB > 0 AND JB < 4 THEN GOTO 824
804 PRINT : PRINT "ENTER 1 for HEWLETT PACKARD PCL language"
806 PRINT "ENTER 2 for KYOCERA EXPRESS language": PRINT "ENTER 3 for ADOBE POSTSCRIPT language"
808 PRINT "OR ENTER 4 TO EXIT WITHOUT PRINTING": INPUT JB: JB = INT(JB): IF JB = 4 THEN LS = 0: RETURN
810 IF JB <= 0 OR JB > 3 THEN SOUND 50, 2: GOTO 804 ELSE QR = 118.1102: REM CONVERT cm to 300 dots
812 PRINT "PRINTER?": IF JB = 1 THEN OPEN "LPT1" FOR OUTPUT AS #4: PRINT #4, CHR$(27); "E"; : RETURN
814 IF JB = 2 THEN LPRINT "!R! FRPO P1,6;UNIT C;SPD .04;SPO P;SLM .1;SRM 21;STM .1;SBM 30;": RETURN
816 INPUT "WHICH COMMUNICATIONS PORT? DEFAULT IS COM1: ENTER 1 OR 2"; CM
818 PRINT "PRINTER CONNECTED?": IF CM < 1 OR CM > 2 THEN CM = 1
820 OPEN "COM" + RIGHT$(STR$(CM), 1) + ":9600,N,8,1,DS,CD,OP" FOR OUTPUT AS #3
822 PRINT #3, "%!": PRINT #3, "0.24 0.24 scale": PRINT #3, "newpath": RETURN
824 IF DOTL = 1 THEN 828 ELSE IF DOTL = 2 THEN 832 ELSE IF DOTL = 3 THEN 868 ELSE IF DOTL = 4 THEN 912
826 IF DOTL = 5 THEN GOTO 942 ELSE STOP
828 IF JB = 2 THEN LPRINT "SPD"; PD; ";"
830 IF JB = 3 THEN LW = INT(PD * QR) - 1: PRINT #3, LW; "setlinewidth": RETURN ELSE RETURN
832 FOR X = LE TO LE + XA * SCX + .1 STEP XA / (GX - 1) * SCX
834 IF JB = 1 THEN PRINT #4, CHR$(27); "*p"; X * QR; "x"; (BP - (BY + YA * SCY)) * QR; "Y"; ELSE 838
836 PRINT #4, CHR$(27); "*c"; ABS((BP - BY) - (BP - (BY + YA * SCY))) * QR; "b"; .05 * QR; "A";
838 IF JB = 2 THEN LPRINT "MAP"; X; ","; BP - BY; ";DAP"; X; ","; BP - (BY + YA * SCY); ";"
840 IF JB = 3 THEN PRINT #3, "newpath" ELSE IF JB = 1 THEN PRINT #4, CHR$(27); "*c0P"
842 IF JB = 3 THEN PRINT #3, INT(X * QR); INT((30 - (BP - BY)) * QR); "moveto"
844 IF JB = 3 THEN PRINT #3, INT(X * QR); INT((30 - (BP - (BY + YA * SCY))) * QR); "lineto"
846 IF JB = 3 THEN PRINT #3, "stroke"
848 NEXT
850 FOR Y = BY TO BY + YA * SCY + .1 STEP YA / (GY - 1) * SCY
852 IF JB = 1 THEN PRINT #4, CHR$(27); "*p"; LE * QR; "x"; (BP - Y) * QR; "Y";
854 IF JB = 1 THEN PRINT #4, CHR$(27); "*c"; .05 * QR; "b"; ABS(LE - (LE + XA * SCX)) * QR; "A";
856 IF JB = 2 THEN LPRINT "MAP"; LE; ","; BP - Y; ";DAP"; LE + XA * SCX; ","; BP - Y; ";"
858 IF JB = 3 THEN PRINT #3, "newpath" ELSE IF JB = 1 THEN PRINT #4, CHR$(27); "*c0P"
860 IF JB = 3 THEN PRINT #3, INT(LE * QR); INT((30 - (BP - Y)) * QR); "moveto"
862 IF JB = 3 THEN PRINT #3, INT((LE + XA * SCX) * QR); INT((30 - (BP - Y)) * QR); "lineto"
864 IF JB = 3 THEN PRINT #3, "stroke"
866 NEXT: RETURN
868 IF JB = 2 THEN LPRINT "SPD .06;"
870 IF JB = 3 THEN LW = INT(.13 * QR): PRINT #3, LW; "setlinewidth": PRINT #3, 1; "setlinecap"
872 FOR W = 1 TO NB: A = LE + X(W) * SCX
874 IF JB = 1 THEN GOSUB 894
876 IF JB = 2 THEN LPRINT "MAP"; A; ","; BP - (BY + Y(W) * SCY); ";CIR"; .05; ";"
878 IF JB = 3 THEN PRINT #3, "newpath"
880 IF JB = 3 THEN PRINT #3, INT(A * QR); INT((30 - (BP - (BY + Y(W) * SCY))) * QR); "moveto"
882 IF JB = 3 THEN PRINT #3, INT(A * QR) + 1; INT((30 - (BP - (BY + Y(W) * SCY))) * QR); "lineto"
884 IF JB = 3 THEN PRINT #3, "stroke"
886 NEXT
888 IF JB = 2 THEN LPRINT "SPD .04;"
890 IF JB = 3 THEN LW = INT(.04 * QR) - 1: PRINT #3, LW; "setlinewidth"
892 IF JB = 3 THEN PRINT #3, 0; "setlinecap": RETURN ELSE RETURN
894 AX = A * QR - 1.5 * 2: YY = (BP - (BY + Y(W) * SCY)) * QR - 3.5 * 2: REM HP DOT
896 PRINT #4, CHR$(27); "*p"; AX; "x"; YY; "Y"; : REM MOVE CURSOR
898 PRINT #4, CHR$(27); "*c"; 7 * 2; "b"; 3 * 2; "A"; : PRINT #4, CHR$(27); "*c0P"
900 AX = A * QR - 2.5 * 2: YY = (BP - (BY + Y(W) * SCY)) * QR - 2.5 * 2
902 PRINT #4, CHR$(27); "*p"; AX; "x"; YY; "Y"; : REM MOVE CURSOR
904 PRINT #4, CHR$(27); "*c"; 5 * 2; "b"; 5 * 2; "A"; : PRINT #4, CHR$(27); "*c0P"
906 AX = A * QR - 3.5 * 2: YY = (BP - (BY + Y(W) * SCY)) * QR - 1.5 * 2
908 PRINT #4, CHR$(27); "*p"; AX; "x"; YY; "Y"; : REM MOVE CURSOR
910 PRINT #4, CHR$(27); "*c"; 3 * 2; "b"; 7 * 2; "A"; : PRINT #4, CHR$(27); "*c0P": RETURN
912 A = (W - 1) * VX + LE: B = BP - BY - Z * VY: FOR XX = A TO A + VX + VX / (C * 2) STEP VX / C
914 IF JB = 1 THEN PRINT #4, CHR$(27); "*p"; XX * QR; "x"; B * QR; "Y";
916 IF JB = 1 THEN PRINT #4, CHR$(27); "*c"; ABS(B - (B + VY)) * QR; "b"; .05 * QR; "A";
918 IF JB = 1 THEN PRINT #4, CHR$(27); "*c0P"
920 IF JB = 2 THEN LPRINT "MAP"; XX; ","; B; ";DAP"; XX; ","; B + VY; ";"
922 IF JB = 3 THEN PRINT #3, "newpath": PRINT #3, INT(XX * QR); INT((30 - B) * QR); "moveto"
924 IF JB = 3 THEN PRINT #3, INT(XX * QR); INT((30 - (B + VY)) * QR); "lineto": PRINT #3, "stroke"
926 NEXT: FOR YY = B TO B + VY + VY / (C * 2) STEP VY / C
928 IF JB = 1 THEN PRINT #4, CHR$(27); "*p"; A * QR; "x"; YY * QR; "Y";
930 IF JB = 1 THEN PRINT #4, CHR$(27); "*c"; .05 * QR; "b"; ABS(A - (A + VX)) * QR; "A";
932 IF JB = 1 THEN PRINT #4, CHR$(27); "*c0P"
934 IF JB = 2 THEN LPRINT "MAP"; A; ","; YY; ";DAP"; A + VX; ","; YY; ";"
936 IF JB = 3 THEN PRINT #3, "newpath": PRINT #3, INT(A * QR); INT((30 - YY) * QR); "moveto"
938 IF JB = 3 THEN PRINT #3, INT((A + VX) * QR); INT((30 - YY) * QR); "lineto": PRINT #3, "stroke"
940 NEXT: RETURN
942 IF JB = 1 THEN PRINT #4, CHR$(27); "*p"; 2 * QR; "x"; 25 * QR; "Y"; : PRINT #4, GR$
944 GG$ = "(" + GR$ + ")": IF JB = 2 THEN LPRINT "MAP 2, 25;TEXT '"; GR$; "';PAGE;EXIT;"
946 IF JB = 3 THEN PRINT #3, "/Times-Roman findfont": PRINT #3, 4.1667 * 12; "scalefont setfont"
948 IF JB = 3 THEN PRINT #3, 2 * QR, 2 * QR; "moveto": PRINT #3, GG$; "show": PRINT #3, "showpage"
950 IF JB = 1 THEN PRINT #4, CHR$(27); "E": RETURN ELSE RETURN

home page